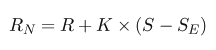El sistema de Ranking Net Dominó 2006
(Basado en el sistema de puntuación ELO)

Los cálculos en el sistema de puntuación ELO se basan en los siguientes principios:
El Score esperado es alto si el ranking del jugador es mayor que el ranking del contrincante, y es bajo si el ranking del jugador es menor que el ranking del contrincante.  Esta propiedad del cálculo del Score esperado tiene consecuencias importantes:
El ajuste del ranking es proporcional a la diferencia entre el score obtenido y el score esperado, usando una constante de proporcionalidad K con un valor de 32 inicialmente, y a medida que el jugador tiene mayor numero de juegos (juegos de ranking), el valor de esta constante K se reduce.  Esto tiene como consecuencia que los jugadores que tienen un alto número de juegos tendrán un ranking mas "estable", que no cambiará drásticamente por haber ganado o perdido un juego.

Las fórmulas utilizadas para el cálculo de cada uno de los parámetros son las siguientes:

Score obtenido:

Para cada jugador, el score obtenido (S) se calcula en función de la puntuación del equipo del jugador (PA) y de la puntuación del equipo contrario (PB), utilizando la siguiente fórmula:

Esta fórmula indica que al ganar un juego se obtiene automáticamente un score de 0.55, más una cantidad proporcional a la diferencia de puntos.  Si uno gana un juego con una diferencia de 100 puntos, el score que uno obtiene es 1.  Por otro lado, el contrincante en ese caso pierde el juego, con lo cual tiene un score de 0.45 menos una cantidad proporcional a la diferencia de puntos;  el score del contrincante en este ejemplo seria de 0  (al perder por una diferencia de 100 puntos).

Score esperado:

Para cada jugador, el score esperado (SE) se calcula en función del ranking promedio del equipo del jugador (RA) y el ranking promedio del equipo contrario (RB), utilizando la siguiente fórmula:


Ajuste del ranking:

Una vez determinados, para cada jugador, el score obtenido (S) y el score esperado (SE), se determina el nuevo ranking de cada jugador (RN) en función del ranking "actual" (el ranking antes de completarse el juego, R), utilizando la siguiente fórmula:


Donde el valor de K se determina para cada jugador en función del número de juegos de ranking que ha completado el jugador (NG):


Ejemplo:

Para ilustrar el cálculo del ranking de cada jugador luego de un juego, usamos como ejemplo un juego entre los jugadores JA y JC contra los jugadores JB y JD.  Los valores de ranking, antes de completar el juego, son: RA: 1680,  RC: 1700,  RB: 1740,  RD: 1700.  El juego terminó a favor de los jugadores JA y JC con una puntuación de 120 - 80.

El jugador JA tiene un total (acumulado del año) de 15 juegos de ranking completados.  El jugador JB tiene un total de 70 juegos de ranking.  El jugador JC un total de 120 juegos de ranking, y el jugador JD un total de 18 juegos de ranking.

Los nuevos rankings de cada jugador se determinan como sigue:

1 –  Se determina el ranking promedio de cada equipo:
RAC = (RA + RC) / 2  =  (1680 + 1700) / 2  =  1690
RBD = (RB + RD) / 2  =  (1740 + 1700) / 2  =  1720

2 –  Se determinan los scores esperados para cada jugador.  En la fórmula para el cálculo de SE, el valor RA se refiere al ranking promedio del equipo del jugador que se está considerando, y el valor RB se refiere al ranking del equipo contrario.  Para los jugadores JA y JC, el valor RA es 1690 y el valor RB es 1720.  Para los jugadores JB y JD, el valor RA es 1720 y el valor RB es 1690.

Los scores esperados son:
Jugadores JA y JC:    SE  =  1 / (1 + 10(1720 – 1690) / 400)  ≈  0.457
Jugadores JB y JD:    SE  =  1 / (1 + 10(1690 – 1720) / 400)  ≈  0.543

Los números arriba tienen sentido:  el equipo JB y JD tienen un ranking más alto, así que se espera (o se estima) que obtendrán, en promedio, un score más alto.

3 –  Se determinan los scores obtenidos para cada jugador.  Los jugadores del equipo ganador (JA y JC) obtienen un score  SG y los jugadores del equipo perdedor (JB y JD) obtienen un score SP:
SG  =  0.55 + 0.45 × (120 – 80) / 100  =  0.73
SP  =  0.45 – 0.45 × (120 – 80) / 100  =  0.27

4 –  Se ajustan los valores de ranking de cada jugador, para lo cual es necesario determinar la constante de ajuste K para cada jugador (en función del número de juegos de ranking de cada jugador):
KA  =  32       (el jugador JA tiene menos de 20 juegos)
KB  =  5 + 4000 / (130 + 70)  =  25
KC  =  5 + 4000 / (130 + 120)  =  21
KD  =  32       (el jugador JD tiene menos de 20 juegos)

Finalmente, se aplica a cada jugador la fórmula de ajuste de ranking:
RA  =  RA(inicial) + KA × (SG – SE(A))  =  1680 + 32 × (0.73 – 0.457)  ≈  1688.74

RB  =  1740 + 25 × (0.27 – 0.543)  =  1740 – 6.825  ≈  1733.2

RC  =  1700 + 21 × (0.73 – 0.457)  =  1700 + 5.733  ≈  1705.7

RD  =  1700 + 32 × (0.27 – 0.543)  =  1700 – 8.736  ≈  1691.3